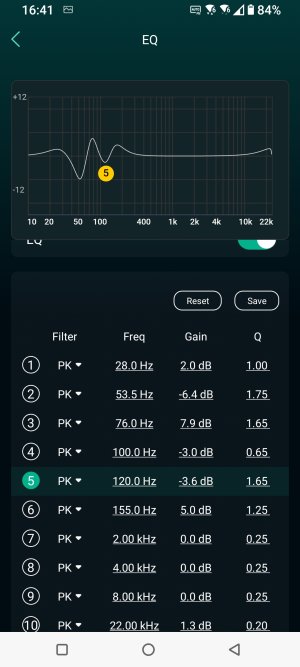
View attachment 8072
Hello. Since I don't have rew or any other software, I would like to ask how, for example, in the case of the settings shown in the attached picture, how can I calculate the percentage by which I should reduce the gain. Thanks.
Turho76,
I wrote a Python script and calculated the impulse response.
With the current PEQ setting, you need -0.93dB pre-EQ gain to avoid clipping. If you are fine with removing filters #7-#10, you need -0.00044884373667138284dB (i.e. 0dB).
Below is a Python script - it works in Windows, Mac OS and etc. Forum does not allow attaching a Python script so I dump as below.
import numpy as np
from scipy.signal import lfilter
# reference:
https://webaudio.github.io/Audio-EQ-Cookbook/audio-eq-cookbook.html
def parametric_eq(bands, fs, pregain):
# Initialize impulse response
impulse = np.zeros(1000)
impulse[0] = 1.0*pow(10,pregain/20)
for band in bands:
filter_type, center_freq, gain, Q = band
A = pow(10,gain/40)
omega = 2*np.pi*center_freq / fs
cos_omega = np.cos(omega)
sin_omega = np.sin(omega)
alpha = sin_omega / (2*Q)
# Define filter types
if filter_type == 'low_shelf':
b0 = A*((A+1) - (A-1)*cos_omega + 2*np.sqrt(A)*alpha)
b1 = 2*A*((A-1) - (A+1)*cos_omega)
b2 = A*((A+1) - (A-1)*cos_omega - 2*np.sqrt(A)*alpha)
a0 = (A+1) + (A-1)*cos_omega + 2*np.sqrt(A)*alpha
a1 = -2*((A-1) + (A+1)*cos_omega)
a2 = (A+1) + (A-1)*cos_omega - 2*np.sqrt(A)*alpha
elif filter_type == 'high_shelf':
b0 = A*((A+1) + (A-1)*cos_omega + 2*np.sqrt(A)*alpha)
b1 = -2*A*((A-1) + (A+1)*cos_omega)
b2 = A*((A+1) + (A-1)*cos_omega - 2*np.sqrt(A)*alpha)
a0 = (A+1) - (A-1)*cos_omega + 2*np.sqrt(A)*alpha
a1 = 2*((A-1) - (A+1)*cos_omega)
a2 = (A+1) - (A-1)*cos_omega - 2*np.sqrt(A)*alpha
elif filter_type == 'peaking':
b0 = 1 + alpha*A
b1 = -2*cos_omega
b2 = 1 - alpha*A
a0 = 1 + alpha/A
a1 = -2*cos_omega
a2 = 1 - alpha/A
elif filter_type == 'low_pass':
b0 = (1 - cos_omega)/2
b1 = 1 - cos_omega
b2 = (1 - cos_omega)/2
a0 = 1 + alpha
a1 = -2*cos_omega
a2 = 1 - alpha
elif filter_type == 'high_pass':
b0 = (1 + cos_omega)/2
b1 = -(1 + cos_omega)
b2 = (1 + cos_omega)/2
a0 = 1 + alpha
a1 = -2*cos_omega
a2 = 1 - alpha
elif filter_type == 'band_pass':
b0 = Q*alpha
b1 = 0
b2 = -Q*alpha
a0 = 1 + alpha
a1 = -2*cos_omega
a2 = 1 - alpha
elif filter_type == 'all_pass':
b0 = 1 - alpha
b1 = -2*cos_omega
b2 = 1 + alpha
a0 = 1 + alpha
a1 = -2*cos_omega
a2 = 1 - alpha
elif filter_type == 'notch':
b0 = 1
b1 = -2*cos_omega
b2 = 1
a0 = 1 + alpha
a1 = -2*cos_omega
a2 = 1 - alpha
else:
raise ValueError('Invalid filter type. Choose either "low_shelf", "high_shelf", or "peaking".')
# Normalize filter coefficients
b = [b0 / a0, b1 / a0, b2 / a0]
a = [a0 / a0, a1 / a0, a2 / a0]
# Calculate impulse response for this band and add to total response
response = lfilter(b, a, impulse)
impulse = response
print([center_freq,min(impulse),max(impulse)])
return impulse
bands = [('peaking', 28.0, 2.0, 1.00),
('peaking', 53.5, -6.4, 1.75),
('peaking', 76.0, 7.9, 1.65),
('peaking', 100.0, -3.0, 0.65),
('peaking', 120.0, -3.6, 1.65),
('peaking', 155.0, 5.0, 1.25),
('peaking', 2000.0, 0.0, 0.25),
('peaking', 4000.0, 0.0, 0.25),
('peaking', 8000.0, 0.0, 0.25),
('peaking',22000.0, 1.3, 0.20)]
response = parametric_eq(bands, 96000,0)
20*np.log10(max(response))
bands_trunc = [('peaking', 28.0, 2.0, 1.00),
('peaking', 53.5, -6.4, 1.75),
('peaking', 76.0, 7.9, 1.65),
('peaking', 100.0, -3.0, 0.65),
('peaking', 120.0, -3.6, 1.65),
('peaking', 155.0, 5.0, 1.25)]
response_trunc = parametric_eq(bands_trunc, 96000,0)
20*np.log10(max(response))